今回はいよいよLEDに接続する抵抗値の計算をします。
今回の説明内容
前々回、前回で電子回路の基本となるオームの法則とキルヒホッフの法則を確認しました。今回はこれらの法則を元にLEDに接続する抵抗値の計算をします。
今回の説明内容は以下になります。
- オームの法則・キルヒホッフの法則の確認
- LEDに接続する抵抗値の計算の流れ
- LEDの特性
- LEDに接続する抵抗値の理想的な計算方法
- LEDに接続する抵抗値の実際の計算方法
- 計算しない方法
- 今回使う抵抗を330Ωにした理由
オームの法則・キルヒホッフの法則の確認
LEDに接続する抵抗値の計算に入る前に、オームの法則とキルヒホッフの第二法則を復習しておきます。
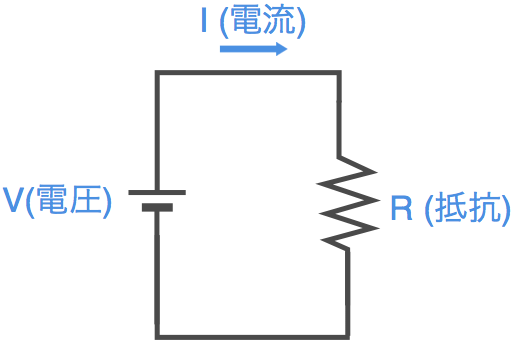
まずオームの法則は、以下の電子回路において、
以下の式が成立する、という内容でした。
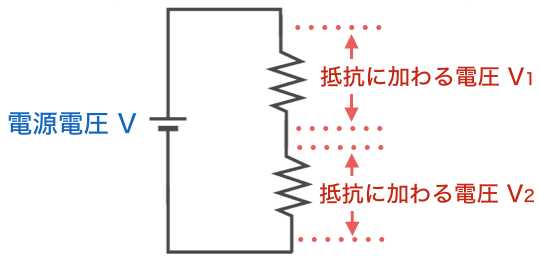
キルヒホッフの第二法則は、以下のような回路において、
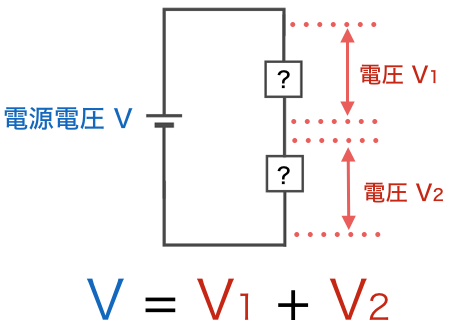
電源電圧とそれに接続される抵抗の電圧の合計は同じ、というものでした。
なおキルヒホッフの法則は、抵抗だけでなくどのような電子部品でも成り立ちます。
LEDの抵抗値の計算は、この2つの法則をもとに進めることになります。
LEDに接続する抵抗値の計算の流れ
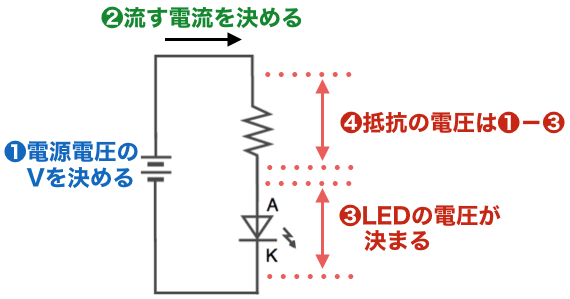
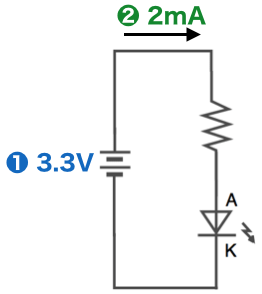
LEDに抵抗を接続して光らせる電子回路として、以下のものを考えます。
この時、LEDに接続する抵抗値は以下の流れで計算します。
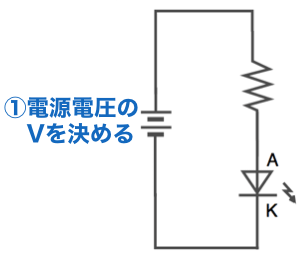
1) 電圧を決める
最初に電源の電圧を決めます。Raspberry PiのGPIOでLEDを光らせる場合、電圧は3.3Vになりますので、3.3Vで計算することになります。
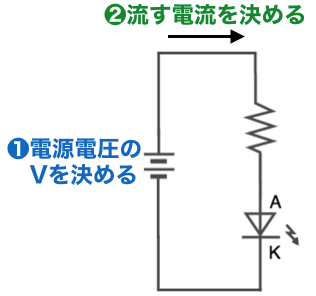
2) 流す電流を決める
次に流す電流を決めます。LEDは流す電流の大きさで明るさが決まります。高輝度LEDの場合は数mAもあれば十分な明るさで光ります。高輝度LEDをたくさん使って照明の目的で使用する場合は20mAぐらい流した方がいいですが、今回は情報を表示するだけですので、2mA程度で計算します
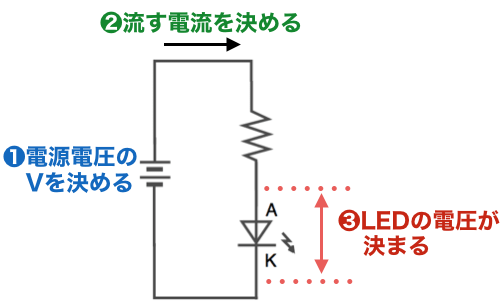
3) LEDに加わる電圧を確認する
LEDの特性についてはこの後のセクションで詳しく説明しますが、LEDに流す電流を決めると、LEDに加わる電圧が(自動的に)決まります。
4) キルヒホッフの第二法則から抵抗に加わる電圧を計算する
電源電圧とLEDに加わる電圧がわかりましたので、キルヒホッフの第二法則から抵抗に加わる電圧を計算します。(1)の電源電圧から(3)のLEDに加わる電圧を引くと抵抗に加わる電圧が求められます。
5) オームの法則から抵抗値を計算する
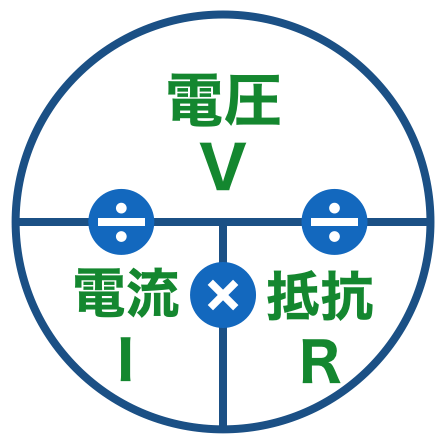
(2)で抵抗に流れる電流が決まり、(4)で抵抗に加わる電圧が決まりましたので、オームの法則から「R = V ÷ I」で抵抗値が計算できます。
それではこの後、LEDの特性を説明した後、実際に抵抗値を求めてみます。
LEDの特性
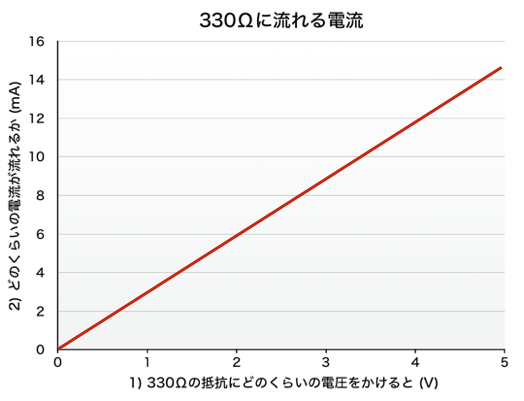
抵抗とLEDの特性は大きく異なります。抵抗はオームの法則に従い、加えた電圧に比例して電流が流れます。例えば330Ωの抵抗の両端にどのくらいの電圧を加えると、どのくらいの電流が流れるか、グラフにすると以下のようになります。
電圧を高くすると、それに比例して電流が多く流れる、というグラフになります。これが抵抗の電圧-電流特性になります。
ところで、LEDは抵抗とは全く異なる性質を持つため、オームの法則はLEDでは成立しません。それではLEDの電圧-電流特性はどうなるのでしょうか。
これから、LEDにどのぐらいの電圧を加えると、どのぐらいの電流が流れるか、実際に実験してみます。この実験は手持ちの部品と安価な測定器で計測しましたので、誤差が多少ありますが、一般的な電子工作であれば問題ない範囲だと思います。
LEDは以下の発光色が白のものを使用しました。
電源としては、電圧を調整できるものを使い、2台のマルチメーター(電圧や電流、抵抗など複数の項目が測定できる測定器)で電圧と電流を測定します。
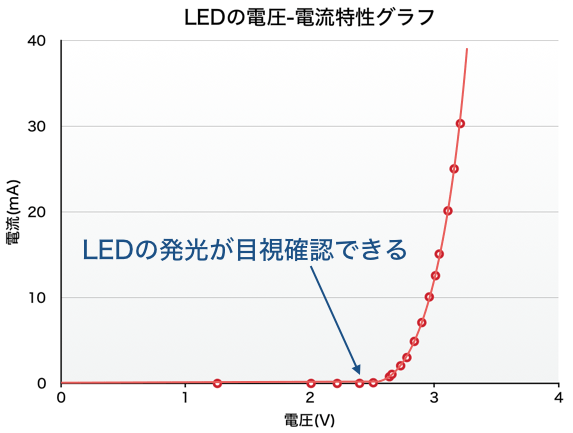
結果は以下のようになりました。
抵抗と全く異なり、電圧を上げていってもしばらくの間は電流がほとんど流れません。2.4Vぐらいから目視でなんとかわかる程度に光り始めます。その後電圧を高くしていくと急激に電流が増えて明るく光るようになります。
なお、光り始める電圧や、急激に電流が増加する電圧は、LEDの種類ごとに異なります。
LEDの特性が分かりましたので、いよいよ実際の数値で抵抗値の計算をしてみましょう。
LEDに接続する抵抗値の理想的な計算方法
それでは、抵抗値を計算してみます。この方法は理想的な計算方法になります。「理想的」という意味は説明の最後で明らかになります。それでは先ほどの手順で計算しましょう!
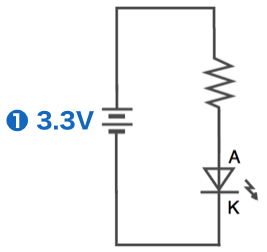
1) 電圧を決める
Raspberry Piの3.3V電源端子を使用しますので、電圧は3.3Vです。
2) 流す電流を決める
情報表示用に光っていることが確認できればいいので、2mAにします。
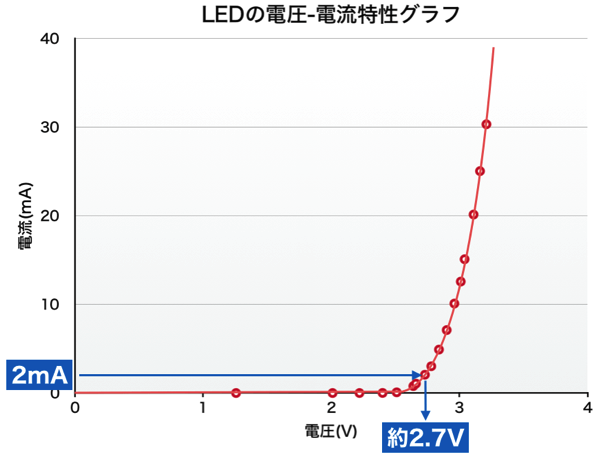
3) LEDの加わる電圧を確認する
先ほど、LEDに加える電圧とその時に流れる電流の特性を調べました。その特性のグラフから、2mA流れる時の電圧をグラフから読み取ると、約2.7Vになります。
ということで、LEDの電圧がわかりました。
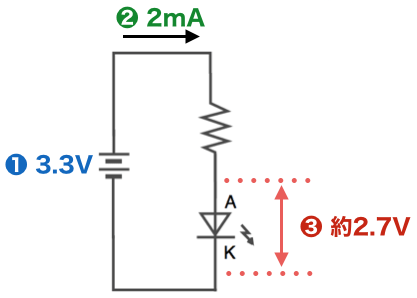
4) キルヒホッフの第二法則から抵抗に加わる電圧を計算する
電源電圧からLEDに加わる電圧を引けば、抵抗に加わる電圧が求められます。3.3V – 2.7V = 0.6Vとなります。
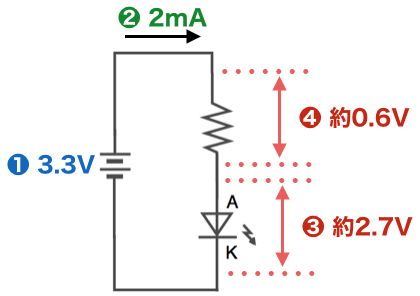
5) オームの法則から抵抗値を計算する
(2)と(4)から、抵抗値は、抵抗 = 電圧 ÷ 電流 = 0.6V ÷ 2mA = 0.6 ÷ 0.002 = 300Ωになります。
これで計算できました!
でもこの計算方法はちょっと問題があります。
実際にLEDを購入する場合、そのLEDの規格の情報が提供されています。上の実験で使用したLEDの規格を確認してみましょう。
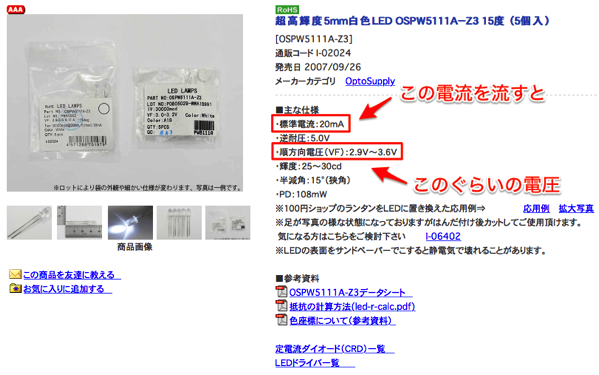
秋月電子通商より引用・加工
これは、電流を20mA流した時、LEDに加わる順方向電圧は2.9V〜3.6Vということを示しています。電流についてはこの表現以外にも「順方向電流」「順電流」「If」などと表記されることもあります。また電圧については、この表現以外にも「順電圧」などと表記される場合もあります。
このLEDの場合は、LEDに流れる電流が20mAの時、LEDに加わる順方向電圧は2.9V〜3.6Vになる、ということなんですが、データとしてはこれだけで、先ほど説明したような電圧と電流の関係を示すグラフは提供されていません。
2mA流したいんですが、2mAの時は何Vなんでしょうかね。また、電流を20mAにする場合でも、順方向電圧は2.9V〜3.6Vって、どの値で計算すればいいのでしょうか。
ということで、先ほど説明した方法はLEDの電圧-電流特性がわかっている場合の計算方法で、実際には電圧-電流特性は示されていないことが大半です。
現実は厳しいもので、LEDに接続する抵抗値を計算する場合、
- LEDの順方向電圧値は、電流が20mAの時の値しか示されていない(泣
- 順方向電圧はばらつきがある(泣
このような状況です。実際には抵抗値をどのように計算したらよいか、次のセクションで説明します。
実際の抵抗値の計算方法
実際の抵抗値の計算方法のポイントは、LEDの順方向電圧をどのくらいの値で計算するか、がポイントになります。
上で説明したLEDを例として使用します。このLEDの特性を整理すると、電流を20mA流す場合、順方向電圧は2.9V〜3.6Vのばらつきがあります。このLEDに2mA程度の電流を流したいときの抵抗値を計算します。
1) 電圧を決める
先ほどと同様、Raspberry Piの電源電圧ピンを使用しますので、3.3Vになります。
2) 流す電流を決める
情報表示用ということで、2mAにします。
3) LEDの加わる電圧を確認する
ここがポイントになります。ポイントといっても経験と勘です。まず、順方向電圧の表示に幅がある場合、データシートを見てみます。
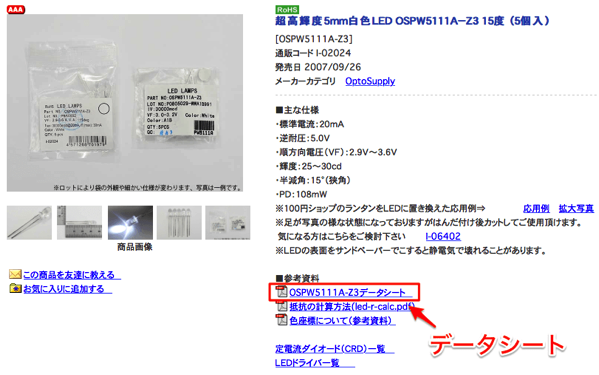
秋月電子通商より引用・加工
データシートの中に、必ず順方向電圧の情報が書かれていますので、それを探します。Vfなどの表記です。
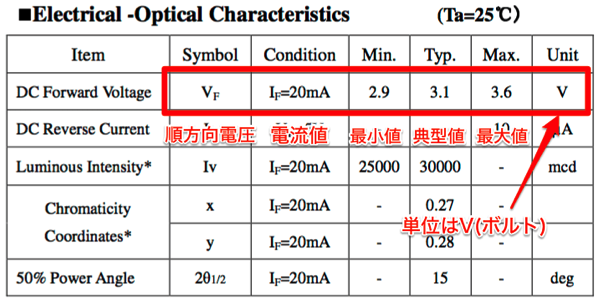
秋月電子通商より引用・加工
この例は、20mA流したときに、順方向電圧の最小値は2.9V、典型値は3.1V、最大値は3.6Vという意味になります。MinはMinimum、TypはTypical、MaxはMaximumの意味です。計算に使用する値はTyp.を使用します。ここでは3.1Vになります。なお、順方向電圧が範囲ではなく、特定の値が表示されている場合はそれが典型値になります。
ところで、電流が20mA流れる時、順方向電圧は3.1Vというのはいいですが、2mA流した時の順方向電圧はどうすればいいでしょうか。これについては経験則で、20mAの順方向電圧値から0.3V〜0.5Vぐらい引いた値にします。0.5Vとすると、3.1V – 0.5V = 2.6Vです。
4) キルヒホッフの第二法則から抵抗に加わる電圧を計算する
電源電圧とLEDに加わる電圧がわかりましたので、キルヒホッフの第二法則から抵抗に加わる電圧を計算します。3.3-2.6=0.7Vとなります。
5) オームの法則から抵抗値を計算する
(2)で抵抗に流れる電流が決まり、(4)で抵抗に加わる電圧を決めましたので、オームの法則から抵抗値を計算します。
0.7 ÷ 0.002 = 350Ω
となります。
抵抗値を計算しない方法
結局LEDの抵抗値の計算方法を見ていると、なんだかあまり根拠のない数字を頼りに計算していることがわかってきましたよね。結局計算してもそれほど正確ではないし、そもそもどれくらいの電流を流すと、どのくらいの明るさで光るのかもよくわからないので、抵抗値の計算はある意味難しいですよね。
そこで、抵抗値を計算しない方法がいくつかあります。
ひとつは、前回の説明で出てきた半固定抵抗を使う方法です。LEDの電流を制限する抵抗値は、電源電圧が3V〜9Vぐらいであれば、だいたい1kΩぐらいまでの抵抗があれば対応できます。そこで、0Ω〜1kΩの間で抵抗値を調整できる半固定抵抗を使う方法があります。
この方法であれば、抵抗値を計算せずに、実際にLEDを光らせてみて明るさを確認しながら抵抗値を調整できます。デメリットとしては部品が高い(1個50円〜100円ぐらい)という点です。
もうひとつは定電流ダイオードを使う方法です。詳しい説明は省略しますが、この部品を抵抗の代わりにLEDに接続すると、特定の電流を流すことができます。
たとえば規格が5mAの定電流ダイオードをLEDに接続すると、電源電圧によらず、5mAの電流になります。ただし、この定電流ダイオードに加える電圧は、ある程度高くないと正常に動作しませんので、Raspberry PiのGPIOピンの3.3Vでは使えないケースもあります。
今まで3回にわたって、オームの法則やらキルヒホッフの法則やらいろいろ確認してきましたが、結果は、計算はちょっと勘に頼っているし、さらに半固定抵抗を使えば計算しなくていいし明るさも確認品が調整できるし、、、って結果になってしまいました。大変な遠回りをしてしまいました。でも、人生、こんなものではないでしょうか。
と言っては身も蓋もありませんが、ここでいろいろ計算したことは、電子回路の基本中の基本、という感じですので、ぜひご自分でもいろいろデータシートを確認したりして計算してみてください。
今回使う抵抗を330Ωにした理由
最後に、今回使う抵抗を330Ωにした理由を説明しておきます。
今回はいろいろなLEDを使います。順方向電圧は発光色によって異なっていて、2V〜3Vぐらいになっています。幅がありますので、とりあえず順方向電圧は2.6〜2.7Vとしました。また電流は2mA程度にします。Raspberry PiのGPIOピンの電圧は3.3Vですので、抵抗に加わる電圧は、3.3 – 2.6〜2.7 = 0.6〜0.7Vとなります。2mA流しますので、抵抗は 電圧 ÷ 電流 = 0.6〜0.7 ÷ 0.02 = 300〜350Ω、ということでその間の330Ωとしました。
また、順方向電圧にばらつきがあるのであれば、半固定抵抗にした方がよかってのではないか、という気もしますよね。ただ、このシリーズでは電子工作をほとんどしたことがない方を想定していますので、なるべくリスクの少ない方法にしています。半固定抵抗は、たとえば1kΩの場合、0Ω〜1kΩの間で調整ができます。もし0ΩにしたままRaspberry Piに接続して電源を入れた場合、GPIOピンからかなりの電流が流れます。その電流によりRaspberry Pi本体とLEDにダメージを与えてしまう可能性もあります。そのため半固定抵抗は使用せず普通の抵抗を使用しました。
電子工作、電子回路に慣れてきたら、いろいろ自分が使える部品を増やしていってみてください。
更新履歴
| 日付 | 内容 |
|---|---|
| 2015.11.21 | 新規投稿 |
| 2019.5.4 | 一部説明変更 |



すごいすごいすごい!これはこのページはどこよりも分かりやすいかもしれないです!キルヒホッフの第二法則はLEDの抵抗計算を調べててこのページでしか見たことがありません!本当にタメになる記事ありがとうございます!!
コメントどうもありがとうございました。
わからないところなどありましたらご質問いただければと思います。