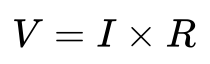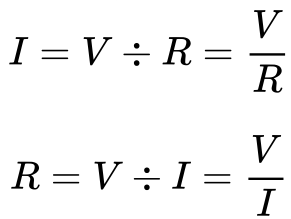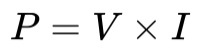LEDに接続する抵抗はどのくらいの値のものをつかえばいいのか、これから3回に分けて説明します。今回は、計算の基本となるオームの法則を説明します。この法則は、Raspberry Piに限らず、電子工作をする上で基本的な考え方になりますので、確実に理解していきましょう!
今回の説明内容
LEDを光らせるためには、電流が流れ過ぎないように電流を制限する必要があることは説明しました。電流を制限する電子部品はいくつかありますが、この入門記事では「抵抗」という部品を使って電流を制限します。
これから3回にわたって、LEDにつなぐ抵抗はどのくらいの値にしたらよいのか、抵抗値の求め方を説明します。なお、説明は長くなると思いますが、長い説明の末の実際のLEDの抵抗値を求る方法は驚くべきものになると思います。
イメージとしては「こんなに長い説明を真面目に読んだのに、そんな仕打ちは許せない!」って感じでしょうか。
ではこれから抵抗の計算をしていきましょう!!
今回の説明内容は以下になります。タイトルを見てもどのような流れで説明されるのか、よくわかりませんよね。今回は実験はありませんので眠くなってしまうかもしれませんが、セクションごと、じっくり読んでいってみてください。
- オームの法則
- 抵抗を探そう!
- もっとオームの法則を使ってみよう!
- 電流の恐怖
- 消費電力も計算しよう!
オームの法則
中学校の理科で「オームの法則」って習ったと思いますが、テストが終わった途端、すぐに忘れてしまった方も多いのではないでしょうか。オームの法則は、単に計算式だけでは済まない話がいろいろありますので、オームの法則の基本に加え、電子工作をする上で重要なところを説明していきたいと思います。
オームの法則は比較的普通の感覚で理解できます。理解するには2つの感覚を確認しておけばよいので、これからその「感覚」について説明します。
最近は照明といえばLED電球が主流になりつつありますが、以前はこのようなタイプの電球がよく使われていましたよね(中身がわかる電球は手持ちでこれしかありませんでした…)。
このような電球は中にフィラメントと呼ばれる電線が入っています。
この電球に電圧を加えると電流が流れてフィラメントの部分が発熱します。フィラメントの発熱温度は数千度と非常に高く、その結果フィラメントが光を放って照明の役割を果たすわけです。
鉄を精製する時、鉄がドロドロに溶けてる場面をテレビなどで見ることがありますが、その時の鉄って光を放っていますよね。あれと同じ原理です。ただしフィラメントは溶けてしまっては照明には使えないので、数千度では溶けないような材料(タングステンという金属)を使っています。
このように電球の中のフィラメントに電圧を与えると電流が流れるわけですが、電圧をだんだん高くしていくと、より多くの電流が流れ、より明るく光ります。逆に電圧をだんだん低くしていくと、流れる電流は少なくなり、光が弱くなっていきます。
これがひとつ目の「感覚」です。電流の流れ方は、電圧に比例して多くなったり少なくなったりする、というのはなんとなく普通の感覚ではないでしょうか。
ところで、上の例では電球を例にとりましたが、他にも電圧を加えると電流が流れる物質はたくさんあります。家電の電源コードに使われている電線などは当然ですが、他には身近なところですとシャーペンの芯も電圧をかけると電流が流れます。
この電線とシャーペンの芯ですが、同じ電圧をかけても同じ大きさの電流が流れるわけではありません。電流の流れやすさは物質の性質により様々で、電線は非常に電流が流れやすいですが、シャーペンの芯はそれに比べると流れにくい性質を持っています。
この電流の流れやすさ(流れにくさ)を抵抗と呼び、流れやすい場合を「抵抗が小さい」、流れにくい場合を「抵抗が大きい」と言っています。同じ電圧を加えても、抵抗が小さい物質は多くの電流が流れ、抵抗が大きい物質は少ない電流が流れます。
これがふたつ目の感覚です。電流の流れ方は、抵抗に反比例して多くなったり少なくなったりする、というのも普通の感覚ではないでしょうか。
例えば水泳を例にとると、早く泳ぐために水の抵抗がなるべく少なくなるように水着を改良したりなど、いろいろ工夫をしてますよね。泳ぐときの抵抗が少ないと早く、抵抗が大きいと遅くなり、泳ぐ速度は水の抵抗に反比例しています。
この2つの感覚からも分かる通り、電圧と電流と抵抗の間には密接な関係があります。この関係を式で表したのが「オームの法則」になります。オームの法則は式で表現されますが、上のような感覚も大切ですので、頭の片隅に置いておいてください。
それではオームの法則の式を説明していきます。これから変数を使っていきますが、今後もいろいろなところで変数による計算式が出てくるので慣れてない方はこれを機会に慣れてみましょう。
| 変数 | 意味 | 単位 |
|---|---|---|
| V | 電圧 | V (ボルト) |
| I (アイ) | 電流 | A (アンペア) |
| R | 抵抗 | Ω (オーム) |
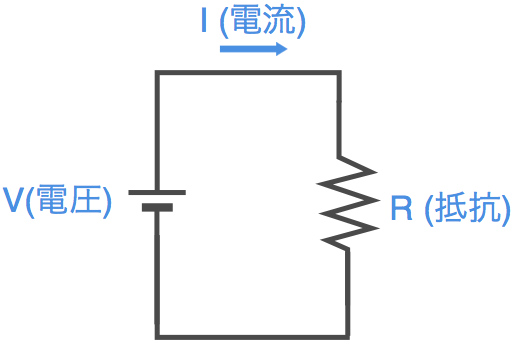
このように変数を定義した時、以下の回路を考えます。
この回路の電圧、電流、抵抗の関係は以下の式で表現でき、これが「オームの法則」になります。
なお、「V = I x R」という式は電圧を求める式になっていますが、この式を変形すると、電流と抵抗は以下の式で表現できます。
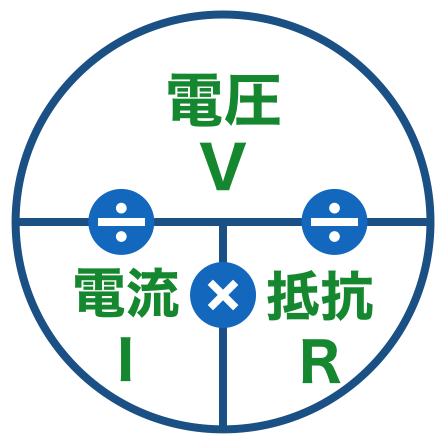
でもこんな似たり寄ったりの式は覚えられないので、以下のような「オームの法則ルーレット」を使います。以下の図は一般的によく使われているものですが、「オームの法則ルーレット」という呼び名は私が勝手に使っているものです。外でうっかり「オームの法則ルーレットが、」なんて言わないように気をつけていただければと思います。
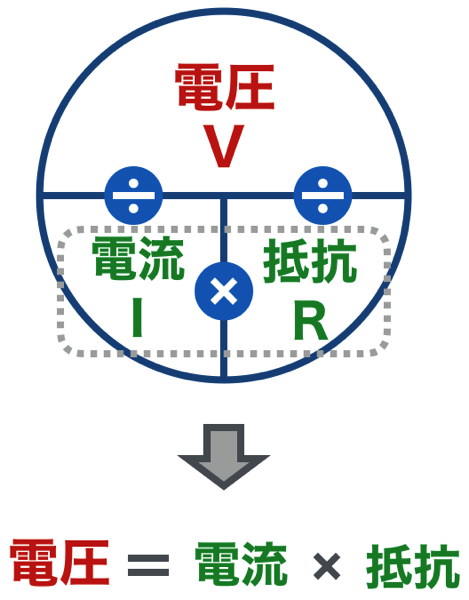
このルーレットの使い方ですが、求めたい値を隠すと残った値で計算できる、というものです。例えば電圧を求めたい場合は、電圧を隠すと(図では赤文字にしています)、残ったところが計算式になります。
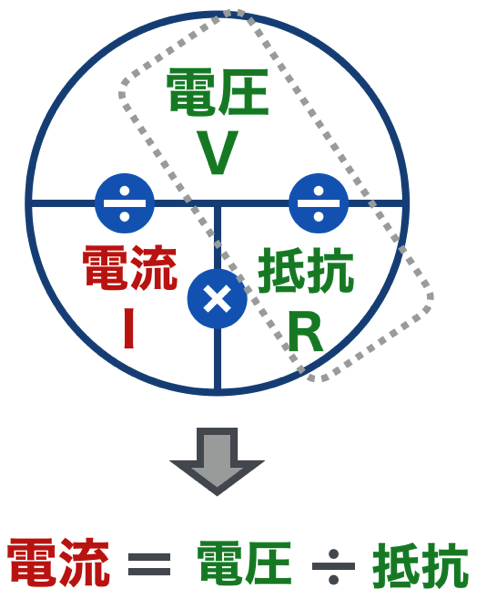
電流を求めたい場合は、以下のようになります。
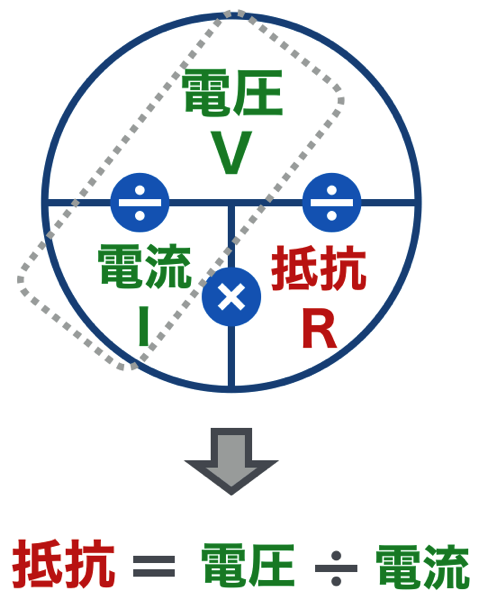
同様に抵抗を求めたい場合は、以下です。
ところで、電子工作をする場合、電流はかなり小さい値、抵抗は比較的大きい値を使うケースが多いです。そのため、補助単位にも慣れておきましょう。補助単位とは、「ミリ」とか「キロ」などのことです。ミリとかキロって普段つかってますよね。例えば「500ml (ミリリッ トル)のペットボトル」とか「ゴールまであと4.5km(キロメートル)」とか。
この「ミリ」とか「キロ」は以下の意味でしたよね。
1ミリ = 1/1000 (1000分の1) = 0.001
1キロ = 1000
このように定義されていますので、以下のように計算します。
| 変換 | 計算 |
|---|---|
| ミリ→普通の単位 | 1000で割る、あるいは0.001を掛ける 例: 50mA = 0.05A (50 ÷ 1000) |
| 普通の単位→ミリ | 1000を掛ける 例: 0.3A = 300mA (0.3 x 1000) |
| キロ→普通の単位 | 1000を掛ける 例: 1.5kg = 1500g (1.5 x 1000) |
| 普通の単位→キロ | 1000で割る、あるいは0.001を掛ける 例: 300g = 0.3kg (300 ÷ 1000) |
これらの変換ができるようにしておきましょう。
ちょっと練習しておきます。
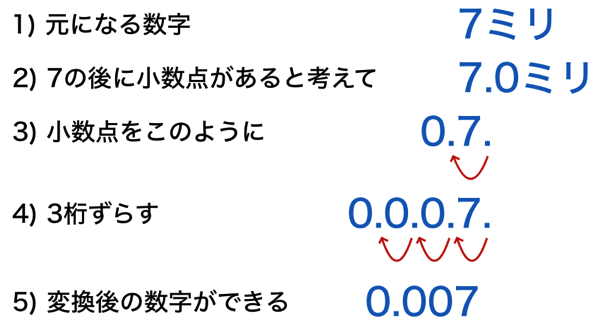
まず、ミリから普通の単位にする場合です。7mA(ミリアンペア)をA(アンペア)表記に変換してみます。ミリから普通に変換するには、計算機であれば1000で割ればOKです。7を1000で割ると、0.007になりますので、7mA = 0.007Aとなります。計算機が手元にない場合は以下のように考えるとよいと思います。
次は、キロから普通の単位にする場合です。0.82kΩ(キロオーム)をΩ(オーム)表記に変換してみます。キロから普通の単位に変換するには、計算機であれば1000をかければOKです。0.82に1000を掛けると、820になりますので、0.82kΩ = 820Ωとなります。計算機が手元にない場合は以下のように考えるとよいと思います。
できれば計算機なしで計算できるようにしましょう。
なお、補助単位をつけたまま以下のように計算することもできます。補助単位はそのままにして数字だけ計算します。
計算結果に以下のようなルールで補助単位をつければOKです。いずれも片方のみに補助単位がある場合です。両方に補助単位がある場合は結果が変わります。
まずは掛け算です。
次に割り算です。
う~ん、ややこしいですね。結局、計算機で計算すればいいのでここまで理解しなくてもいいですが、計算機なしで早く計算できるようになると電子回路の計算が楽になりますよ。
抵抗を探そう!
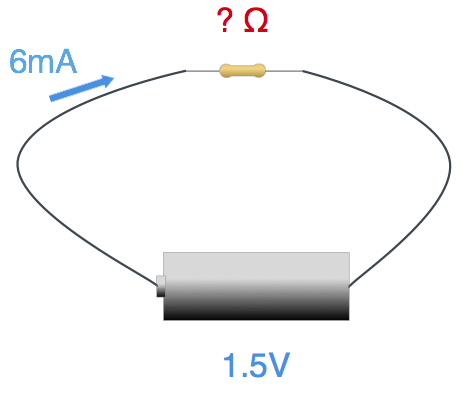
それでは、具体的にオームの法則を使ってみましょう。例として、単三乾電池(使い捨てタイプ)に抵抗を接続して6mAを流したい場合、抵抗はどのぐらいにすればよいか計算してみます。単三乾電池は使い捨てタイプですので電圧は1.5Vとして計算します。実体配線図は以下のようになります。
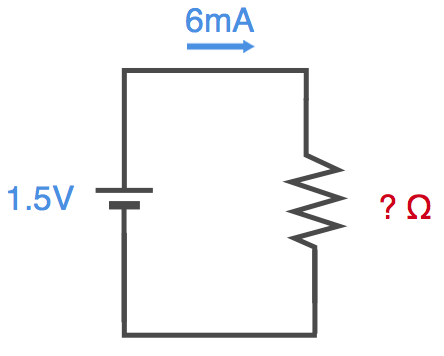
これに対応する電子回路は以下のようになります。
抵抗の値は「オームの法則ルーレット」を使うと、以下のように計算できますが、
抵抗 = 電圧 ÷ 電流
電圧の単位はV、電流の単位はAですので、6mAは0.006Aに変換しておきます。この式に当てはめて計算すると、
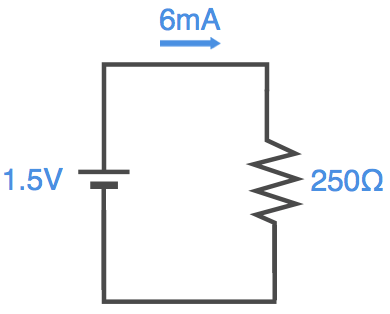
抵抗 = 1.5 ÷ 0.006 = 250
ということで「250Ω」が答えです。
それでは、もうちょっとオームの法則を使って計算に慣れていきましょう。最初の方で説明した2つの感覚について確認しておきます。
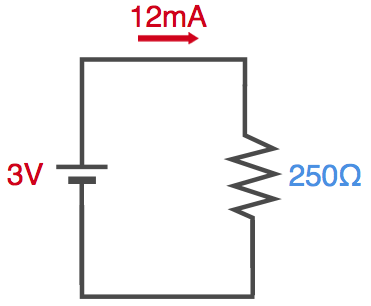
ひとつ目は「電圧を高くすると、より多くの電流が流れる」です。上の回路はこのような値です。
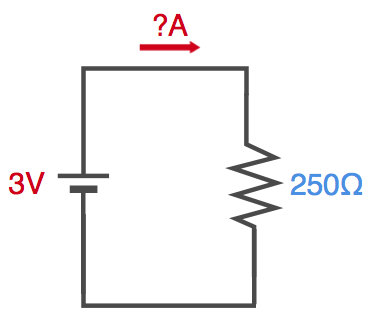
この回路で電圧を倍の3Vにしてみます。このとき電流はどのくらいになるか計算してみます。
電流 = 電圧 ÷ 抵抗
ですので、
電流 = 3 ÷ 250 = 0.012A = 12mA
となります。
電圧を2倍にしたら、電流も2倍になりましたよね。
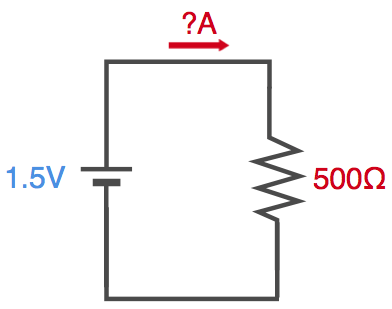
それでは次にふたつ目の感覚、「同じ電圧を加えた場合、抵抗が小さい場合は多くの電流が流れ、抵抗が大きい場合は少ない電流が流れる」を確認してみます。
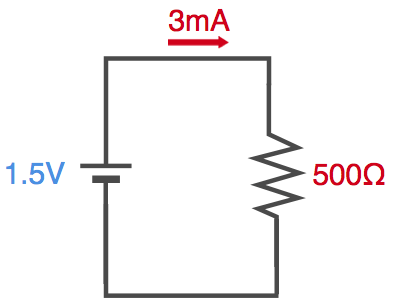
先ほどの回路で、抵抗を250Ωから500Ωにした場合、どのくらいの電流が流れるでしょうか。
電流 = 1.5 ÷ 500 = = 0.003A = 3mA
となります。
なんか計算は飽きてきましたので次に進みましょう。
一番最初の回路ですが、250Ωの抵抗を用意すれば良いことがわかりましたので、さっそく250Ωの抵抗をネットショップで探してみましょう!
なんて言ってみましたが、実際に250Ωの抵抗を探しても、どこのネットショップでも売っていないんです!
実は、抵抗は飛び飛びの値しか用意されていません。どれくらい飛び飛びか、というのは規格で決められています。また飛び飛び具合については、いくつかの系列が用意されています。と言葉で説明してもよくわいらなので、もうちょっと具体的に確認してみます。まず系列についてはwikipediaに説明がありますので確認してみてください。
いきなり数字の羅列ばかりですが、表のタイトルのところを見ると、「E3」「E6」「E12」…とあります。これがそれぞれ系列で、抵抗で一般に使われているのは「E24系列」になります。E24系列の欄を見ると
10, 11, 12 ,13, 15, 16, 18, 20, 22, 24, 27 … 82, 91
とありますよね。この系列の抵抗は、この数字を0.1倍、1倍、10倍、100倍…した値のものが用意されていることになります。例えば「22」という数字がありますが、この数字をもとに、0.1倍の2.2オーム、1倍の22Ω、10倍の220Ω、100倍の2200Ω=2.2kΩ…がある、という意味です。
ということで、今回探している抵抗は250Ωですので、「25」という数字が欲しいところですが、E24系列にはなく、結果、抵抗として250Ωのものはない、ということになります。
なお、E24系列の抵抗でも、これら全ての数字の0.1倍、1倍、10倍、100倍、、、という全ての抵抗が製造されているわけではあまりせんので、実際に入手可能な抵抗かは確認が必要です。
では、計算した値の抵抗がない場合はどうすればいいのでしょうか。その場合は、設計する電子回路の仕様に問題がなければ一番近い値の抵抗を使用します。またどうしてもその値にしたい場合は抵抗を組み合わせて使用します。抵抗の組み合わせ方は次回の記事で説明します。
もっとオームの法則を使ってみよう!
もうちょっとオームの法則を使ってみましょう。
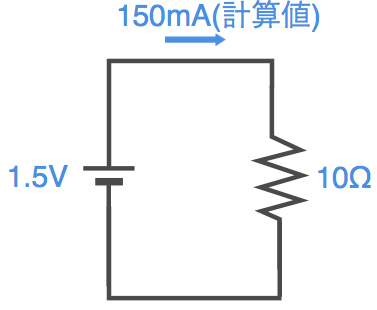
例として、使い捨てタイプの単三乾電池1本に10Ωの抵抗を接続した場合の電流値はどのくらいになるか計算してみます。まず最初に計算で電流値を求めておきましょう。
I = V ÷ R = 1.5 ÷ 10 = 0.15A = 150mA
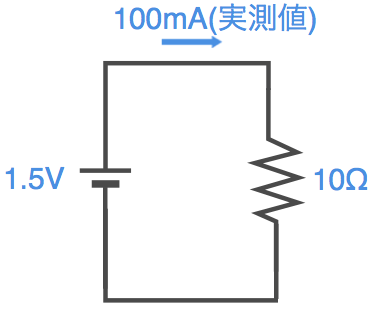
となります。電池の電圧はぴったり1.5Vではないですし、抵抗も若干の誤差がありますが、それでもだいたい150mAぐらい流れるってことですよね。それでは実際に電池と抵抗を接続して測定器で電流を測定してみます。
あれ? 計算上では150mAになるはずでしたが、実際に測定すると93.7mAって、これだけ差があると計測誤差の範囲を超えてますよね。これってどういうことなのでしょうか。
これは、どのような電源であっても、流すことのできる電流に限界があるためです。電池も、いくらでも電流が流せるわけではありません。一般的な単三乾電池ではこの程度が限界だと思います。将来、例えばLEDをたくさん点灯させる電子回路を設計するときに、オームの法則で計算するだけでなく、このようなことも考慮して設計する必要がある、ということを覚えておきましょう。
なお、Raspberry Piの電源用にUSBアダプタを用意したと思います。自分は5V/2.4Aのものを用意しました。これは、出力電圧は5Vで、電流は2.4Aまで流す能力があるよ、ってことを意味しています。
電流の恐怖
ところで、先ほどの実験で電池から流れる電流は最大で100mA程度、つまり0.1A程度でしたが、電池ってこんなに少ししか電流がながれないんだ、って思いませんでしたか? USB電源アダプタの2.4Aに比べてずいぶん少ないなぁ、なんて思いませんか?
100mAって微々たるものって感じがしますが、実際はかなり危険な電流なんです。では、どのくらいの電流が人体に流れると、どのくらいの影響があるか、まとめたサイトがありますので、見てみましょう。
このページの真ん中あたりに、どのくらいの電流で、どのような人体影響があるかが表にまとめられています。100mAのところを見ると「心室細動の発生、心肺停止、極めて危険な状態に」ってあります。ちょっとビリビリ痺れる、というレベルではないですよね。一歩間違えば、、、という内容です。
ん? 先ほどの実験では電池で100mAぐらい流れましたよね。ということは、この電池を手で持ったら、あの世に行ってしまうんでしょうか。でも実際は電池を手で持っても平気ですよね。ではなぜ大丈夫なのかわかりますか?
実は人間の体も抵抗がありますが、その抵抗が非常に大きいためほとんど電流が流れないためです。身体が抵抗、ということは、オームの法則を使えば身体に流れる電流が計算できますよね。電圧は1.5Vですのであとは抵抗がわかれば流れる電流の値を求めることができます。
それでは実際に測ってみます。今回は電池を人差し指と親指で挟むように持つとして、人差し指と親指の抵抗を測定してみます。
手の状態(どのくらい湿っているかなど)でかなり変わってきますが、この測定ではだいたい5MΩ(メガオーム) = 5000000Ωでした。このときの電流は、
電流 = 1.5 ÷ 5000000 = 0.0000003A = 0.3μA(マイクロアンペア) = 0.0003mA(ミリアンペア)
です。先ほどの厚生労働省のサイトによると、最小感知電流は0.5mA〜1mA程度とのことですので、感じることのできる最小の電流のさらに1万分の1ぐらいの電流しか流れない、ということになります。
ただし、手が濡れている場合などはもっと抵抗が少なくなります。よく、濡れた手で電気製品を触らないように、という注意書きがあるのは、手が濡れると身体の抵抗が低くなるので、電流が流れやすくなって危険なためです。ご参考に、先ほどと同じ測定方法で手を濡らして抵抗を測定したところ、約0.5MΩでした。今回の測定では手をぬらすと抵抗は10分の1程度になりました。
消費電力も計算しよう!
ちょっとオームの法則から離れますが、抵抗を扱う上で他にも大切なことがありますので説明します。
ネットショップや店頭で売っている抵抗を見ると、
「カーボン抵抗 1/4W 330Ω ±5%」
「酸化金属被膜抵抗 1W 330Ω ±5%」
などの表示がされています。「なんとか抵抗」の「なんとか」の部分は使用している材料で、材料によって特徴があります。LEDの電流制御には安価なカーボン抵抗で十分ですが、精度が必要だったり、熱に耐える必要がある場合はその目的にあった抵抗を選びます(かなり種類があるので説明は省略します)。次の赤文字の部分がここで説明するものです。
この赤文字部分は許容電力を示しています。抵抗なのに電力? って感じですが、もう一度電球を思い浮かべてみてください。電球のフィラメントは抵抗で、この抵抗に電流を流すと熱が発生して光ると同時に、電力を消費しています。電球が何W、というのは、この消費電力のことになります。当然LEDに接続する抵抗も電球のフィラメントと同じ性質の「抵抗」ですので、光りはしませんが電力を消費します。
つまり上の赤文字部分は、この抵抗の電力の許容値は何Wか、ということを示しています。
もうちょっと細く説明すると、抵抗の許容値は発熱量で決まります。発熱量が大きいと、抵抗がどんどん熱くなりやがては壊れてしまうためです。この発熱量ですが、電力に比例しています。抵抗を表記するとき、発熱量の許容値を書くより、電力の許容値を書いた方かわかりやすいので電力値が書かれています。
この「電力」ですが、単位は「W(ワット)」で、一般に変数は「P」が使用されます。電力をPとすると、以下の式で表現されます。
この入門シリーズで購入した抵抗は「1/4W」という表記です。「1/4」は4分の1ですので、許容電力は0.25W、ということになります。
先ほど、単三乾電池に10Ωの抵抗をつないで、かなり電流を流しましたが、電力は大丈夫だったのでしょうか。ちょっと計算してみます。最初に実測値で計算してみます。1.5Vに10Ωを接続して、実際に電流を測ったところ約100mA流れました。
電力を計算すると、
P = V x I = 1.5V x 0.1A = 0.15W
ということで、許容値が0.25Wですので許容内です。もし単三乾電池ではなく、十分な電流が流せる電源を使用した場合、オームの法則通りに電流が流れますので、
電力を計算すると、
P = V x I = 1.5V x 0.15A = 0.225W
ということで、まだ許容値内ですね。
ところで、カーボン抵抗は1/4Wタイプの他に1/6Wタイプもよく見かけます。1/6Wは0.167Wです。ということは、上の回路に使用した場合、許容値を超えてしまうので使えないことになります。
普通の電子回路では許容値に届くことはそれほどありませんが、例えば照明用のLEDの回路を設計する場合など、電流が大きめの回路の場合は、抵抗の電力許容値も注意するようにしましょう。
[補足]
点灯し続けるような場合は定格電力の半分を目安に設計するのが好ましいです。
更新履歴
| 日付 | 内容 |
|---|---|
| 2015.11.14 | 新規投稿 |
| 2019.5.4 | 一部表現変更 |