次回からいよいよ回路を設計して組み立てていきますが、その際に必要となる知識をもうちょっと確認しておきます。今回はクイズ形式で確認することにしてみます。
今回の説明内容
Raspberry PiのGPIOピンを正確に理解するには、もうちょっと電子回路の知識が必要です。今回はクイズ形式で電子回路に慣れておきます。
今回の説明内容は以下になります。
- オームの法則の別の見方
- 例題
- クイズ – ここの電圧は何V?
- 答え
オームの法則の別の見方
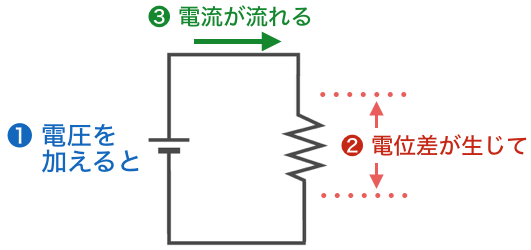
何度も同じことばかりで申し訳ないのですが、オームの法則を使えば、抵抗にどのくらいの電圧を加えるとどのくらいの電流が流れるか計算できます。当たり前ですが、抵抗に電圧を加えると電流が流れる、ということになります。
つまり「抵抗に電圧を加える(=抵抗に電位差があれば)、電流が流れる」ということですよね。
これをもうちょっと別の見方をします。なんとなく言い方の違い、という気もしますが、以下のことが言えます。
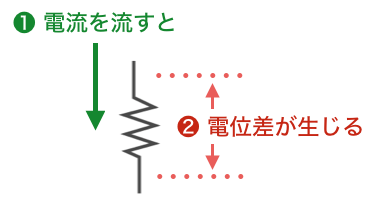
「抵抗に電流を流せば、電位差が発生する」
何を言いたいんだろう、って感じですよね。正直、抵抗に「電位差が生じたから電流が流れる」のか「電流が流れたから電位差が生じたのか」そんなどうでもいいことは他でやってくれ、ってところでしょうか。
この見方で考えると、当たり前ですが、以下のことが言えます。
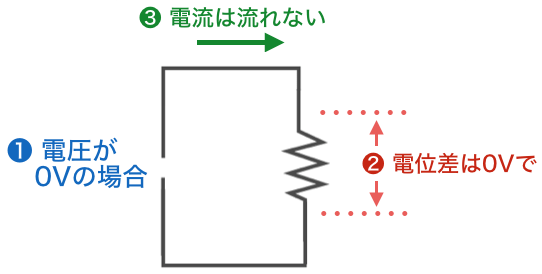
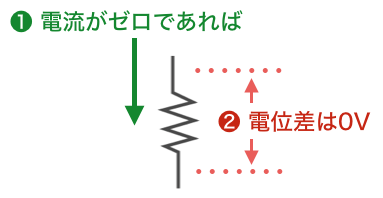
「抵抗に電圧を加えない、つまり電位差がゼロであれば電流は流れない」
これを先ほどの見方で考えると、
「抵抗に電流が流れていなければ、電位差はゼロ」
ということになります。この考え方はとても大切なのですが、言葉だけではなかなか理解が深まらないので、残りは全てクイズ形式にしてみます。答えを見る前に考えてみてください。
例題
まずは例題です。以下の電子回路の赤丸のところはそれぞれ何Vになるでしょうか。
ワイヤで接続されている部分はどこも同じ電圧ですので、A点が3.3V、B点とC点は0Vになります。
それでは、これにスイッチをつけます。
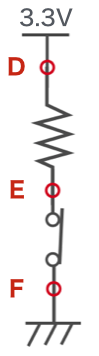
スイッチを閉じた状態の時は、ワイヤで接続した状態と同じですので、先ほどと同じように、D点は3.3V、E点とF点は0Vになります。
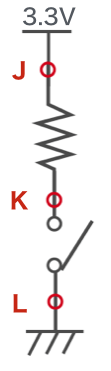
それでは、スイッチを開いた状態にした場合、それぞれ何Vでしょうか。
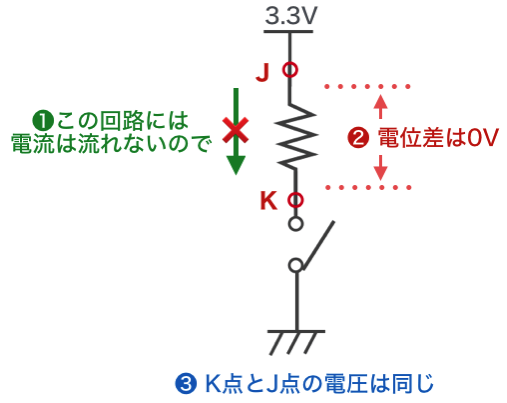
答えはJ点とK点が3.3V、L点が0Vになります。K点の電圧がわかりづらかったのではないでしょうか。これは以下のように考えます。
この回路にはスイッチがあり、開いていますので電流は流れません。当然抵抗にも電流は流れませんので、一番最初に説明した考え方をすると、抵抗の電位差は0Vになります。ということは、K点はJ点と同じ電圧、ということにになりますので、K点の電圧は3.3Vとなります。
抵抗の両端の電位差がどうなっているか、という点に注意しながらクイズに挑戦してみてください。
クイズ – ここの電圧は何V?
それぞれの赤丸の地点の電圧は何Vになるでしょうか。
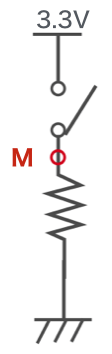
最初は上の回路でスイッチの位置を変えてみたものです。スイッチは開いています。
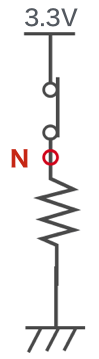
次はこの回路のスイッチを閉じてみました。
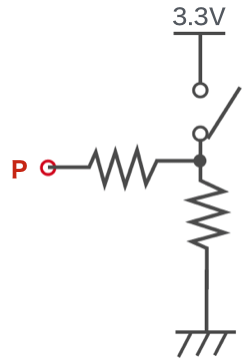
次に、上の回路に抵抗を1本追加してみました。スイッチは開いています。
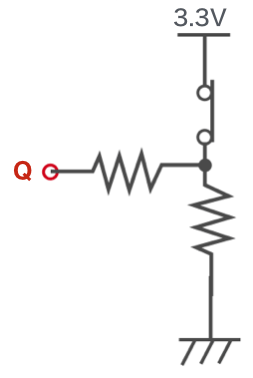
この回路のスイッチを閉じてみます。
抵抗に電流が流れるのかがわかれば解けそうですよね。
答え
答えは以下になります。
| 地点 | 電圧 |
|---|---|
| M | 0V |
| N | 3.3V |
| P | 0V |
| Q | 3.3V |
M点、N点は例題と同じように考えればわかると思います。
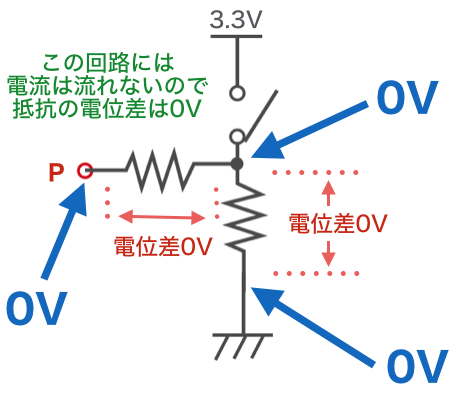
P点は以下のように考えます。
この回路には電流は流れませんので、2本の抵抗の両端の電位差は0V、アースからたどっていけばP点の電圧は0Vであることがわかります。
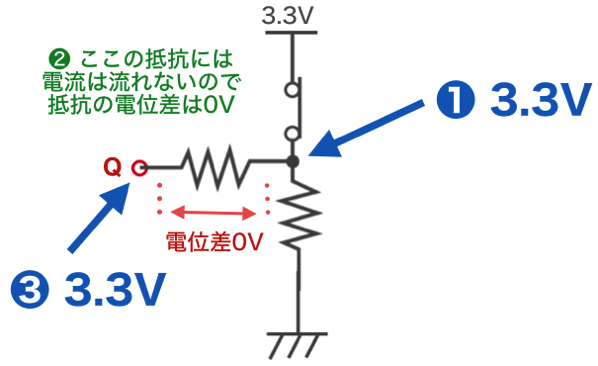
Q点は以下のように考えます。
まず、(1)の地点は3.3Vです。次に、Q点につながっている抵抗には電流は流れませんので、この抵抗の電位差は0Vになります。従って、Q点の電圧は3.3Vとなります。
ちょっと慣れないと分かりづらいかもしれませんが、ポイントは抵抗に電流が流れるかどうか、流れない場合は電位差0Vというところです。
次回はRaspberry PiのGPIOの仕様を説明、回路を組み立てていきますが、今回の考え方がところどころ出てきますので、この考え方を身につけておきましょう。
更新履歴
| 日付 | 内容 |
|---|---|
| 2015.11.21 | 新規投稿 |
| 2019.5.4 | 一部説明補足 |