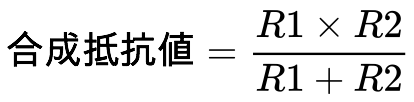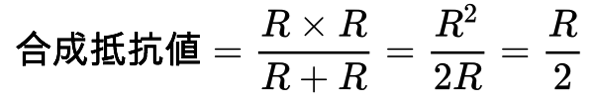LEDに接続する抵抗はどのくらいの値のものをつかえばいいのか、なんだか長い説明になってしまっていますが、今回はキルヒホッフの法則について説明します。まだまだ続きます。
今回の説明内容
前回、電池に抵抗を接続した回路で、希望の電流を流す場合の抵抗の値は、「抵抗=電圧÷電流」で求めました。でもこの式で求めた値の抵抗は必ずしも入手できるわけではないことがわかりました。多くの場合、電子回路上問題がなければ、近い値の抵抗を使用することになります。ただ、微妙な調整が必要な場合など、計算した抵抗値にしなければならないケースもあります。
今回は、求めた値の抵抗がない場合、どうしてもその値の抵抗値にしたい場合にはどうしたらよいか説明します。
ところでタイトルにある「キルヒホッフの法則」ってご存知でしょうか。あまり出てこない言葉ですが、オームの法則に並んで、電子回路を理解する上で基本的な法則になります。オームの法則と同様、感覚でわかると思いますので、今回もじっくり読んでみてください。
今回の説明内容は以下になります。
- 抵抗の組み合わせ方の基本2通り
- 直列接続とキルヒホッフの第二法則
- 並列接続とキルヒホッフの第一法則
- 実際に抵抗を組み合わせる際の注意点
- 補足 – 直列接続と並列接続の抵抗値計算式導出
抵抗の組み合わせ方の基本2通り
唐突ですが、細い短いロープが何本かある場合を考えます。このとき、長いロープが欲しい場合はどうしたらよいでしょうか。その場合は、細い短いロープを結んで長いロープを作ればいいですよね(当たり前)。
では、(強度的に)太いロープが欲しい場合はどうでしょうか。この場合は細いロープが何本かあるので、束ねれば太いロープ相当のものが作れます(当たり前!)。
(いずれも「無料イラスト素材ドットコム」より引用・加工)
話を抵抗に戻します。計算した値の抵抗がない場合、それらをうまく組み合わせれば、計算値に近い値の抵抗を作ることができます。この組み合わせですが、ロープの場合にとても似ています。一つは長いロープを作った時のように、以下のように接続するパターンです。
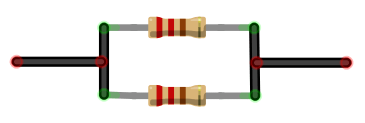
もう一つは太いロープを作った時のように、以下のように接続するパターンです。
抵抗を含めて、電子部品を数珠つなぎのようにつなげていく接続を「直列接続」、並べてつなげていく接続を「並列接続」と呼びます。
このように抵抗を組み合わせることにより、計算値に近い抵抗値にすることが可能になります。ではこれから、抵抗を直接接続した場合と並列接続した場合、抵抗値はどのようになるのかその計算方法を含めて説明します。
直列接続とキルヒホッフの第二法則
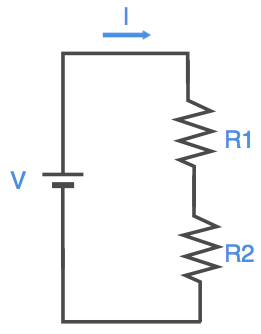
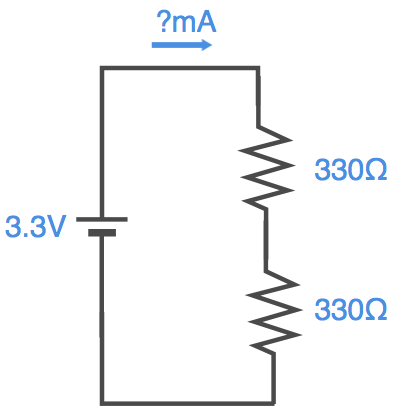
抵抗を2本直列接続にして電池に接続した場合、回路図は以下のようになります。
この時接続する2本の抵抗の値は、それぞれR1、R2(Ω)とします。このように2本の抵抗を直列に接続した場合、組み合わせた抵抗値はどのようになるのでしょうか(このように複数の抵抗を組み合わせて1本の抵抗としてみた時の抵抗を「合成抵抗」と呼んでいます)。
この直列接続の合成抵抗の値は単純な足し算になります。
前回の説明で、250Ωの抵抗は入手できない、と説明しましたが、このように直列接続することにより、250Ωの抵抗が作れるかもしれません。まず、E24系列の値はどうだったか確認すると、
10, 11, 12 ,13, 15, 16, 18, 20, 22, 24, 27 … 82, 91
となっています。24がありますので、240Ωはありそうです。あと10Ωがあれば直列接続すれば250Ωになります。E24系列をもう一度確認すると、10がありますので、10Ωもありそうです。実際にネットで調べてみると、240Ωと10Ωの抵抗が売られていることが確認できます。このケースでは、250Ω = 240Ω + 10Ωで作ることができます。
せっかくですので、直列接続回路を使って、もうちょっと電子回路の理解を深めたいと思います。
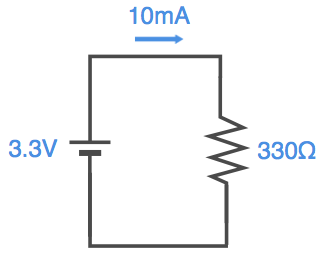
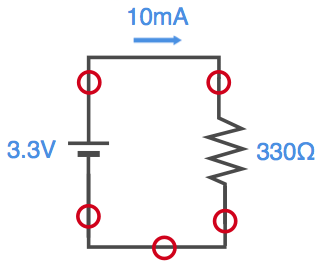
最初に以下のような抵抗が1本の基本回路を考えます。
この回路はオームの法則に従い、3.3Vの電圧、330Ωの抵抗に対して、10mAの電流が流れます。
「10mAの電流が流れます」とは言っても、この回路のどこに10mA流れるのでしょうか。具体的に考えてみましょう。例えば、以下の赤丸のところは何mAの電流が流れているのでしょうか。
答えはすべて10mAです。このように接続線の分岐がなく、1本の接続線で繋がっている回路では、どこの地点の電流も同じになります。抵抗を通った後は電流が少なくなる、とか、電池のプラスから出た直後は電流が一番多い、などということはありません。これが電流の特徴です。念のため確認しておくと、2本の抵抗を直列接続した回路でも、流れる電流はどこの地点も同じです。
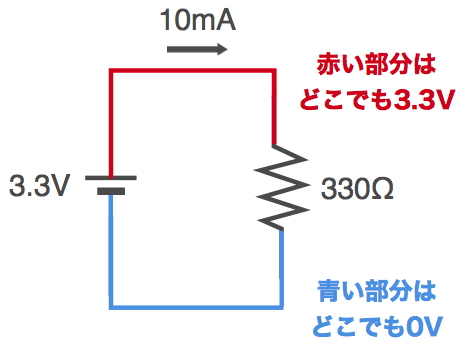
それでは次に電圧について確認しておきます。部品を接続している接続線がありますが、部品間のワイヤの電圧はどこも同じです。例えば以下のようになります。
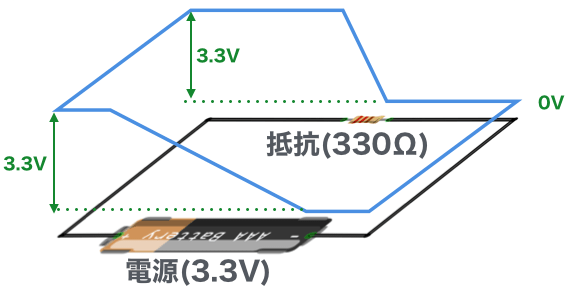
これをもうちょっと立体的に表現すると以下のようになります。電池と抵抗を接続した回路に対して、それぞれの地点の電圧を青い線で高さで表しています。
このように1本の線で閉じている回路を1周すると元の電圧に戻ってきます。また、このように1本の線でぐるっと回って帰ってきた時、通ってきた回路を「閉回路」と呼びます。
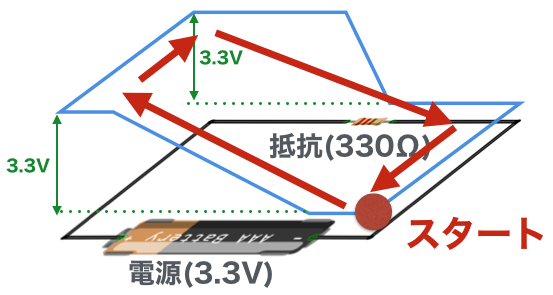
例えば上の図では0Vのところから出発して、電池を通った後は3.3V、そのあと抵抗を通ると0Vに戻り、元のスタート地点に戻ってきます。これは別な見方をすると、閉回路をぐるっと1周まわってきた時、上昇した電圧値と下降した電圧値は同じ、ということも言えます。なんか当たり前のような気がしますよね。でもこれ、とても大切なことなんです。というのは、今回は電池と抵抗の回路でしたが、これはどんな種類の電子部品を何個使った場合でも、すべての電子回路に当てはまります。
この法則は発見者の名前がついていて「キルヒホッフの第二法則」と呼ばれています。でもいきなり「第二法則」ってなんなんですかね。第一法則もあるのでしょうか。それとどうでもいいですが「キルヒホッフ」って発音しづらいですよね。
それではこのキルヒホッフの第二法則を抵抗の直列接続回路でも確認してみます。
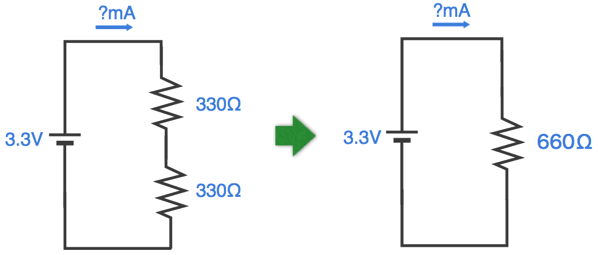
まず、以下の回路を考えます。
この回路に流れる電流を求めてみます。流れる電流を求めるには最初に合成抵抗値を計算します。直列抵抗の合成は単純に足し算をすればいいので、330Ω + 330Ω = 660Ωです。
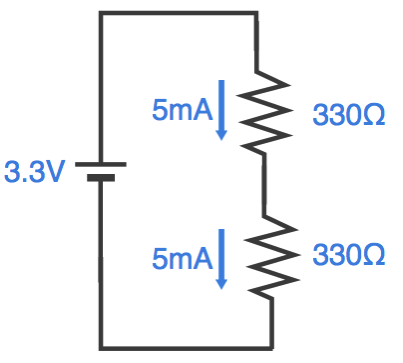
上の右側の回路であれば、いつものオームの法則で電流が計算できます。電流 = 電圧 ÷ 抵抗 = 3.3 ÷ 660 = 0.005A = 5mAとなります。この5mAの電流はどこでも同じですので、当然、両方の抵抗にも同じ電流が流れています。
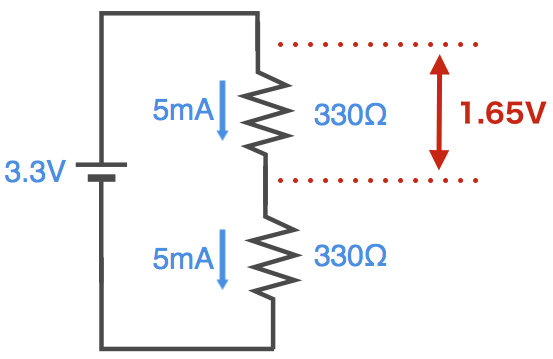
ここでちょっと別の見方をしてみます。オームの法則では「電圧 = 電流 x 抵抗」という式があります。赤枠の部分に注目すると、この330Ωの抵抗には5mAの電流が流れています。ということは、この抵抗には
電圧 = 電流 x 抵抗 = 5mA x 330Ω = 1.65V
という電圧が発生していることにもなります。
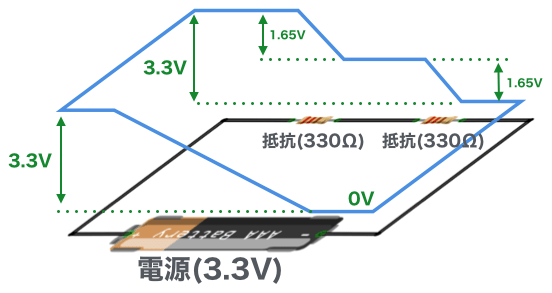
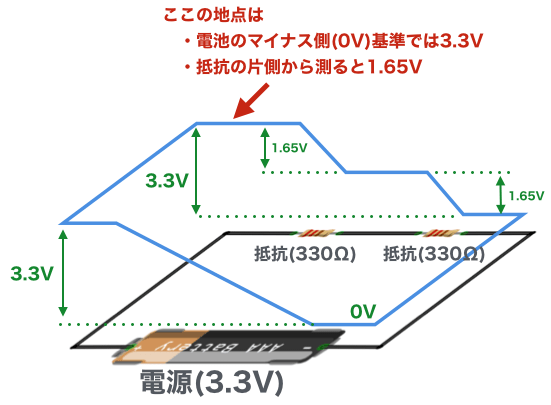
同様にもう一方の330Ωの抵抗にも1.65Vの電圧が発生しています。これをキルヒホッフの第二法則で考えてみると以下のようになります。
今まで、電圧が何V、というような呼び方をしてきましたが、このような直列回路では、同じ地点の電圧が、見方によって異なるケースがあります。
このような状況を正確に表現するために、以下のように呼びます。
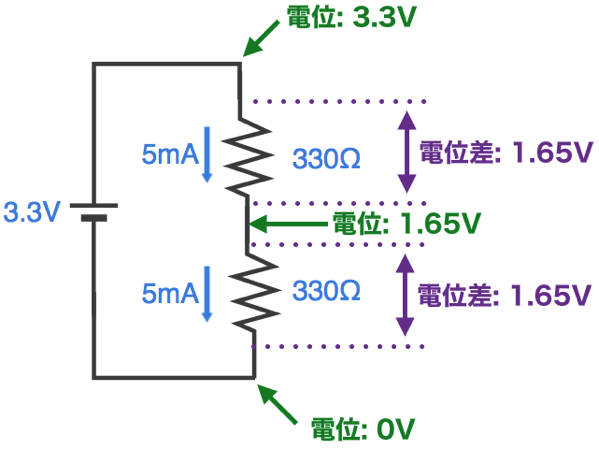
0V基準で計測した電圧を「電位」と呼びます。また抵抗の両端の電位の差を「電位差」と呼びます。上の図を電子回路に置き換えてみます。
「ここの電位は」や「この抵抗両端の電位差は」などの説明が出てきたりしますので、上のような図を思い浮かべてみてください。
もう一度ロープの例と比べると、細い短いロープを直列につなげると、ロープの長さは足し算した長さになります。抵抗を直列に接続すると抵抗の値が足し算した値になります。なとなく雰囲気が似ていますよね。
ところで、同じロープを2本並列に束ねると強度が2倍になります。抵抗を2本並列に接続すると、何がどうなるのか、次に並列接続の回路を確認してみます。
並列接続とキルヒホッフの第一法則
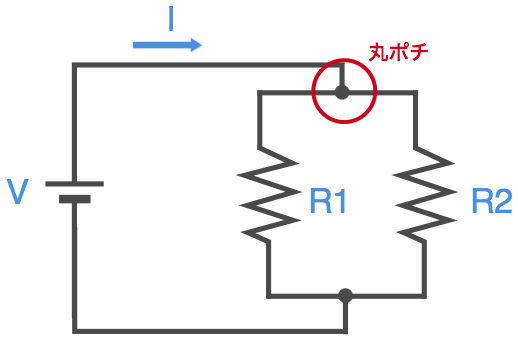
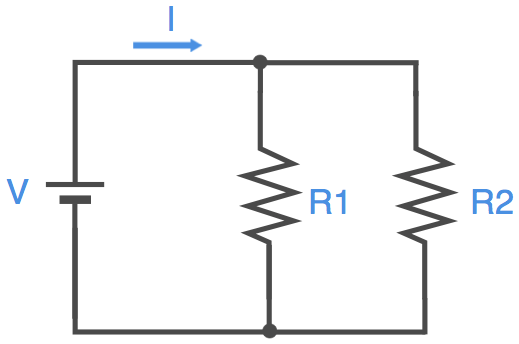
抵抗を2本、並列接続にして電池に接続した場合、回路図は以下のようになります。
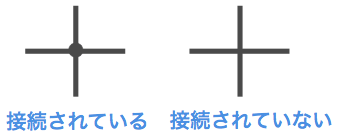
回路図をよく見ると、ワイヤが交わっているところに丸ポチがあります。
これは接続されていることを明確にする表現です。特に十字に交差している場合は注意が必要です。特に回路図を描く場合は忘れがちですので注意します。
なお、この後いろいろ説明図を描く都合で、今後は並列接続の回路図は以下のようにします。
上の2つの並列接続は電気的な接続は同じですので、同じ回路になることを確認してみてください。
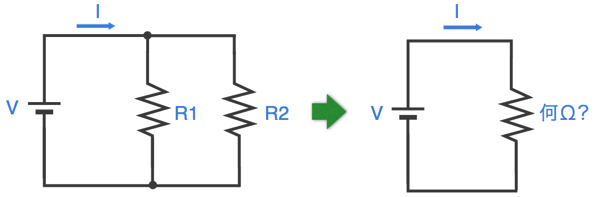
それでは、並列接続の場合、合成抵抗値はどのようになるのでしょうか。
この場合の合成抵抗値は以下のようになります。
、、、、、、、
直列接続の抵抗の場合は、抵抗を単に足し算していけばいいので、例えば250Ωが欲しい場合、入手できる抵抗値をあれこれ足し算していけば計算できます。
でも、並列接続の場合、上の計算式で250Ωになる組み合わせを探すのはかなりきついですよね。上の式で何Ωと何Ωを組み合わせれば250Ωになるのか、直感でわかりませんよね。このように並列接続で抵抗値を調整するのは難しいのですが、同じ抵抗値の抵抗を並列接続した場合は簡単です。抵抗値は半分になります。上の合成抵抗値の式で、R1とR2が両方ともRΩとすると、以下のようになります。
細かいことは置いておいて、同じ抵抗値の抵抗を並列接続すると抵抗値は半分になる、と覚えておけばよいと思います。
だんだん計算するの面倒になってきましたよね。合成抵抗値の計算はこのぐらいにして、並列接続の場合に重要なことを説明します。
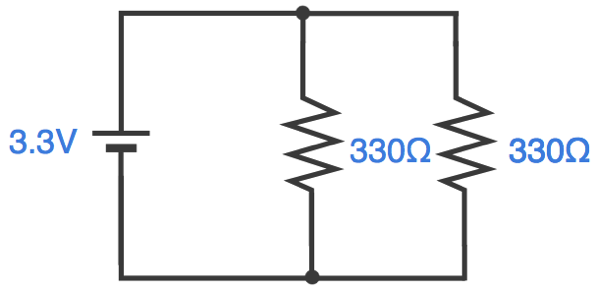
まず、以下の回路を考えます。
まず、この回路の電位を確認してみます。先ほどと同じように電位をかくと、以下のようになります。ポイントは、直列回路の時と同様、部品同士を接続しているワイヤは同じ電位になる点です。
閉回路でキルヒホッフの第二法則が成り立っていることを確認してみてください。(閉回路は3つあります)
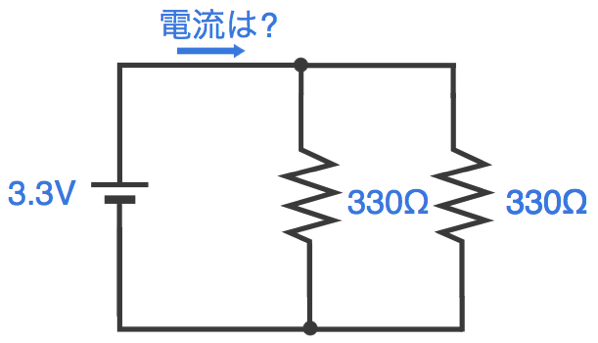
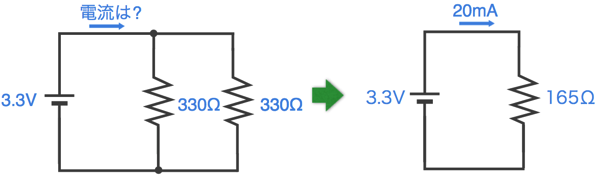
ところで、この回路に流れる電流はどのくらいになるのでしょうか。
先ほどの並列接続の合成抵抗の計算式に当てはめると(というより同じ抵抗なので半分になります)、合成抵抗値は165Ωになります。電源の電圧が3.3V、抵抗が165Ωですので、電流 = 電圧 ÷ 抵抗 = 3.3 ÷ 165 = 0.02A = 20mAになります。
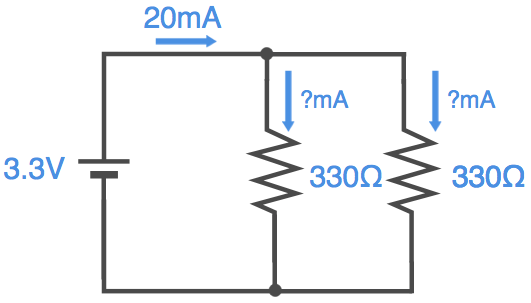
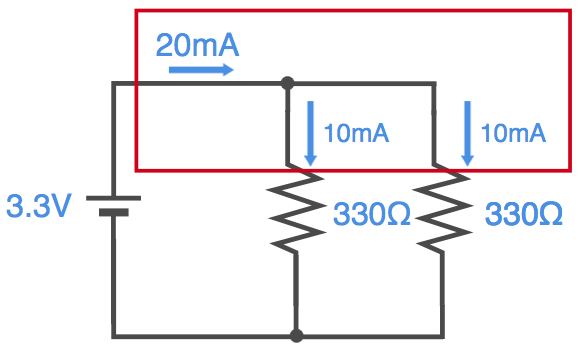
ところで、並列回路は接続しているワイヤが途中で分岐しています。それぞれの抵抗を流れる電流はどのくらいなのでしょうか。
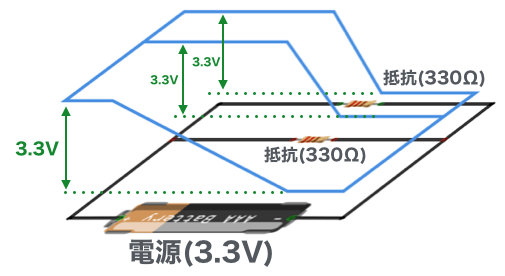
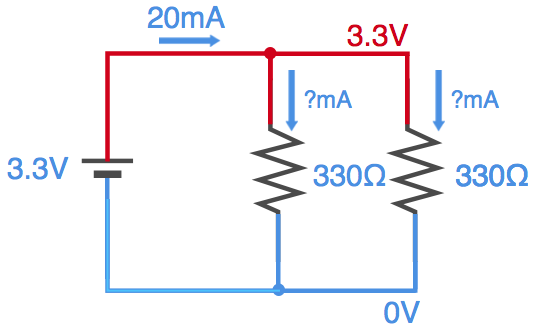
抵抗を流れる電流は、抵抗の両端の電位差がわかれば計算できますよね。部品間のワイヤ線の電位は同じですので、以下の図で、赤いワイヤ線は3.3V、青いワイヤ線は0Vとなります。ということは、両方の抵抗はそれぞれ3.3Vの電圧が加わっています。
ここまでわかればオームの法則で計算できます。電流 = 電圧 ÷ 抵抗 = 3.3 ÷ 330 = 0.01 = 10mAとなります。
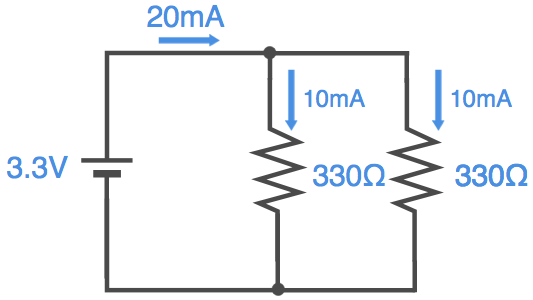
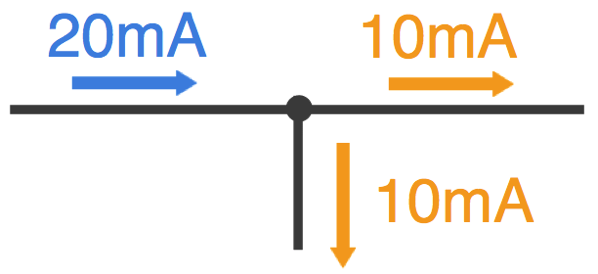
ここで、分岐しているところに注目します。
この分岐点の電流の流れを見ると、分岐点に入ってくる電流は20mA、出て行く電流は10mAが2本となっています。
電流は水の流れに近いので、この現象も理解できますよね。この例では分岐点に入ってくる電流が1本、出て行く電流が2本で、入ってくる電流と出て行く電流の合計は同じ、ということでしたが、これは入ってくる電流の本数と出て行く電流の本数は何本でも成り立ちます。また、これは電池や抵抗に限らず、どんな電子部品でも成り立ちます。これが「キルヒホッフの第一法則」です。
電子回路上では電子部品が並列接続になるケースがたくさんあります。その場合、分岐点の電流の流入合計と流出合計は同じ、という「キルヒホッフの第一法則」が必ず成立しますので、これも是非覚えておいてください。この後の回の説明でもキルヒホッフの第一法則が出てきます。
最後に、ロープの例と比べてみます。同じロープを2本並列に束ねると強度が2倍になります。抵抗を2本並列に接続すると、流れる電流が2倍になる、ということになります。
実際に抵抗を組み合わせる際の注意点
このセクションを読むと、今までの説明は何だったの?、って感じになりますが、今までの説明は電子回路を理解するための理論、とご理解ください。実際にぴったりの抵抗が欲しい場合、抵抗を組み合わせることはあまりありません。
例として、235Ωの抵抗が欲しい場合を考えてみます。E24系列で入手可能な抵抗を探すと、組み合わせとしては、
220Ω + 10Ω + 4.7Ω = 234.7Ω
ということで、ほぼ235Ωになります。ただ、これには問題があります。特定の抵抗値が欲しい、という場合はかなり正確にその値が欲しい状況のはずです。235Ω欲しい場合に、上の組み合わせであれば0.3Ω差なのでほぼ問題ないだろう、という判断ができそうですが、実際は抵抗の誤差を考慮する必要があります。
まず一般的なカーボン抵抗の場合、誤差は±5%です。ということは、220Ωの抵抗の誤差は、220 x 0.05 = 11、ということで、最大11Ωの誤差がある可能性があります。一般に入手しやすい誤差の少ない金属皮膜抵抗でも誤差は±1%です。上の組み合わせの場合、誤差の最大は約2.35Ωになります。
抵抗を組み合わせると誤差の問題が出てきますので、一般的には特定の値の抵抗が欲しい場合は、「可変抵抗器」を使います。可変抵抗器というと聞きなれないですが、一般にはボリュームと呼ばれているものです。ボリュームというと音量を調整する部品のように感じますが、もともとは抵抗を変えることができる電子部品のことです。
なお、電子工作などで特定の抵抗値が欲しい場合、一度抵抗値を調整したらそのあとは変更しないことが多いです。音量調整などに使われる可変抵抗器には指で操作できるつまみがあり、いつでも抵抗値を変えることができますが、抵抗値をほとんど変えないのであればつまみは必要ありません。そのため、指で回せるつまみではなくプラスドライバーなどで回すことのできる調整用のつまみがついた可変抵抗器もあります。これは、一度調整したらそのあとは基本的に固定して使用することから、「半固定抵抗器」と呼ばれています。「半固定ボリューム」「半固定可変抵抗器」とも呼ばれます。
半固定抵抗器も大きく分けて2種類あります。
半固定ボリューム(1kΩ) 秋月電子通商
多回転半固定ボリューム (1kΩ) 秋月電子通商
両方とも1kΩの半固定抵抗器ですが、上はつまみを1回転回すと0Ω〜1kΩの値になります。下はつまみを25回転回すと0Ω〜1kΩの値を取ります。どの程度の精度が欲しいかで使い分けます。
更新履歴
| 日付 | 内容 |
|---|---|
| 2015.11.15 | 新規投稿 |
| 2019.5.4 | 合成抵抗の計算式導出説明を削除 |